Welcome to Sudoku Today!
Today Sudoku contains very many types of variant Sudoku, more types of Sudoku puzzles are still under continuous development, please continue to pay attention to Sudoku today.
Today's Sudoku
9-July-2025
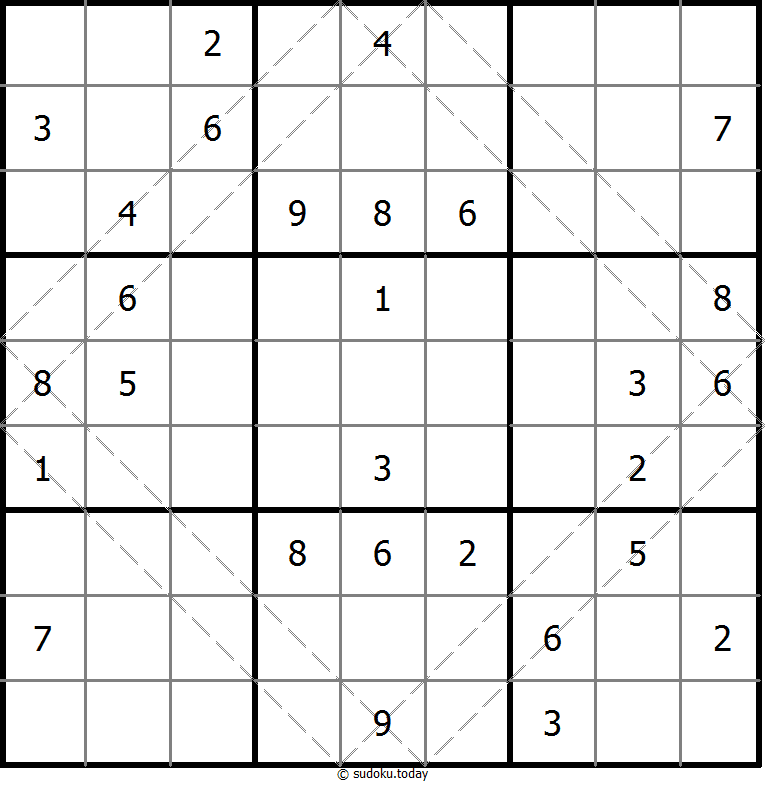
Multi Diagonal Sudoku
- Place a digit from 1 to 9 into each of the empty squares so that each digit appears exactly once in each of the rows, columns and the nine outlined 3x3 regions.
- Digits do not repeat along the marked diagonals.
Multi Diagonal Sudoku
- Place a digit from 1 to 9 into each of the empty squares so that each digit appears exactly once in each of the rows, columns and the nine outlined 3x3 regions.
- Digits do not repeat along the marked diagonals.
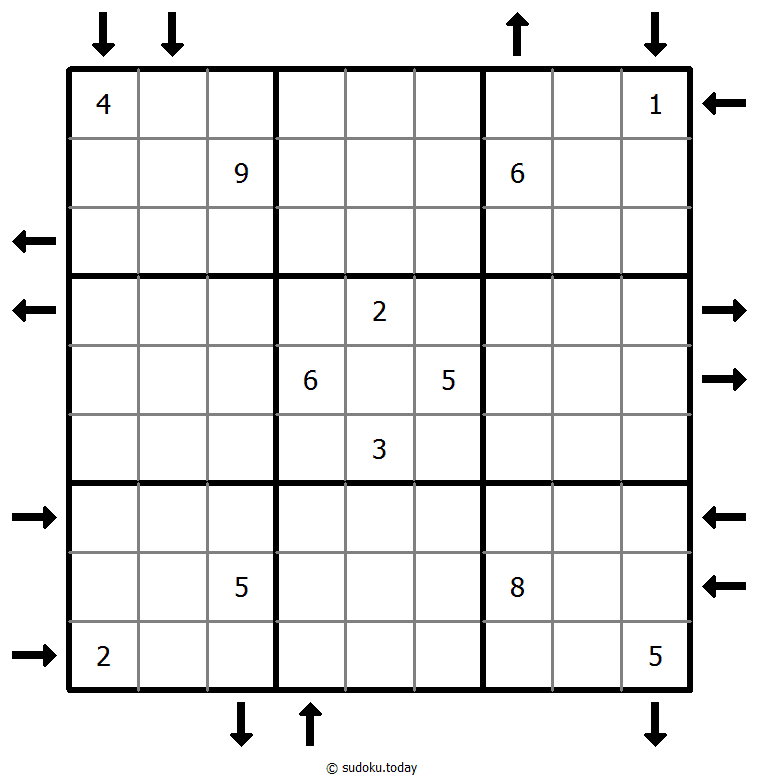
Rossini Sudoku
- Place a digit from 1 to 9 into each of the empty squares so that each digit appears exactly once in each of the rows, columns and the nine outlined 3x3 regions.
- The arrows outside the grid indicate that the nearest three digits in the corresponding direction are in ascending or descending order (the highest number is always in the direction of the arrow). All possible arrows are given, so if there is no arrow, the first three digits do not form an increasing sequence in either direction.
Rossini Sudoku
- Place a digit from 1 to 9 into each of the empty squares so that each digit appears exactly once in each of the rows, columns and the nine outlined 3x3 regions.
- The arrows outside the grid indicate that the nearest three digits in the corresponding direction are in ascending or descending order (the highest number is always in the direction of the arrow). All possible arrows are given, so if there is no arrow, the first three digits do not form an increasing sequence in either direction.
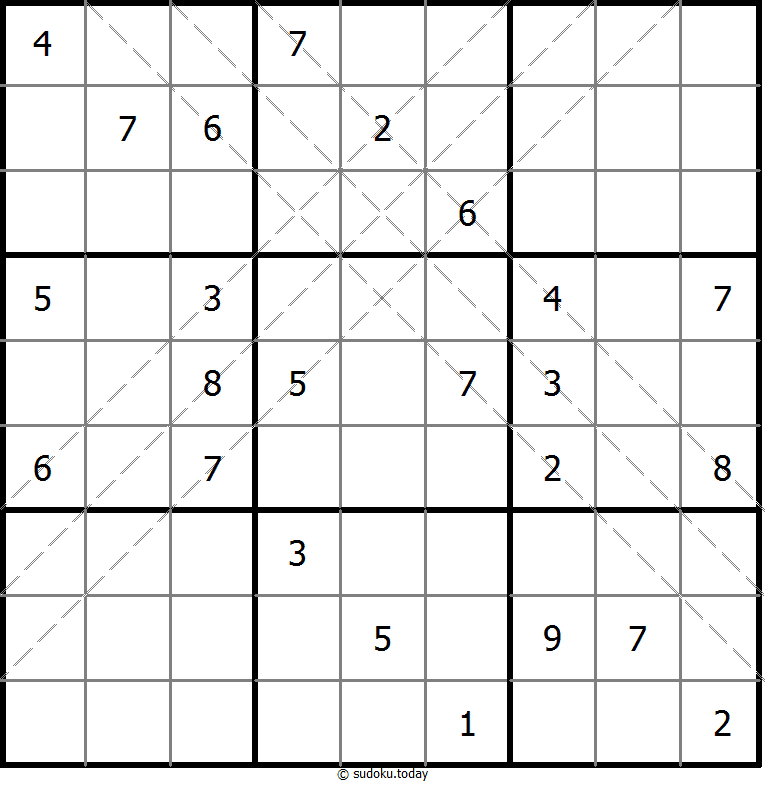
Multi Diagonal Sudoku
- Place a digit from 1 to 9 into each of the empty squares so that each digit appears exactly once in each of the rows, columns and the nine outlined 3x3 regions.
- Digits do not repeat along the marked diagonals.
Multi Diagonal Sudoku
- Place a digit from 1 to 9 into each of the empty squares so that each digit appears exactly once in each of the rows, columns and the nine outlined 3x3 regions.
- Digits do not repeat along the marked diagonals.
Point To Next Sudoku
- Place a digit from 1 to 9 into each of the empty squares so that each digit appears exactly once in each of the rows, columns and the nine outlined 3x3 regions.
- If digit ‘n’ is placed in a cell with an arrow, digit ‘n+1’ must be placed in one of the cells pointed by the arrow.
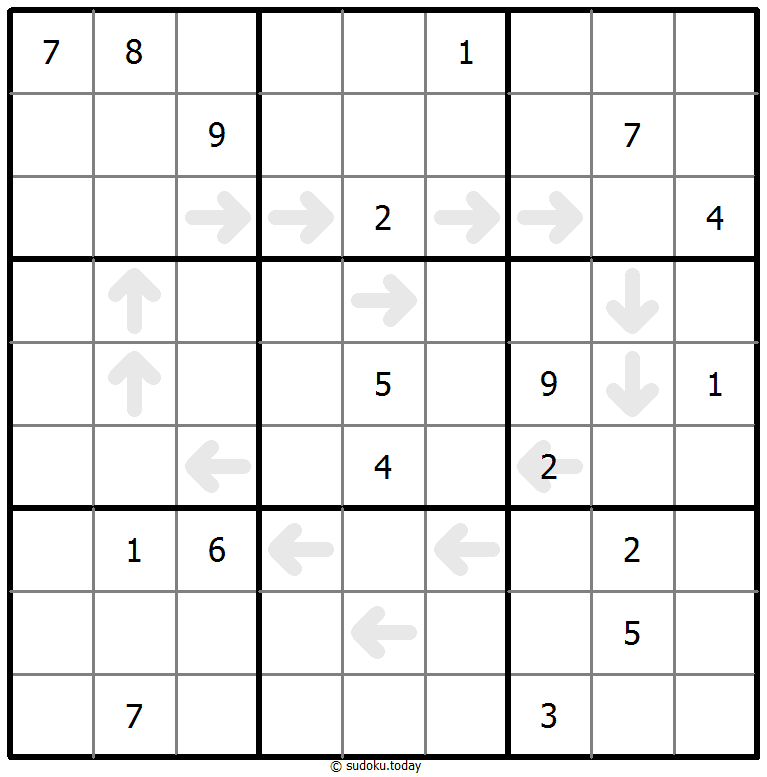
Point To Next Sudoku
- Place a digit from 1 to 9 into each of the empty squares so that each digit appears exactly once in each of the rows, columns and the nine outlined 3x3 regions.
- If digit ‘n’ is placed in a cell with an arrow, digit ‘n+1’ must be placed in one of the cells pointed by the arrow.
X Sums Sudoku
- Place a digit from 1 to 9 into each of the empty squares so that each digit appears exactly once in each of the rows, columns and the nine outlined 3x3 regions.
- Each number outside the grid is the sum of the first X numbers placed in the corresponding direction, where X is equal to the first number placed in that direction.
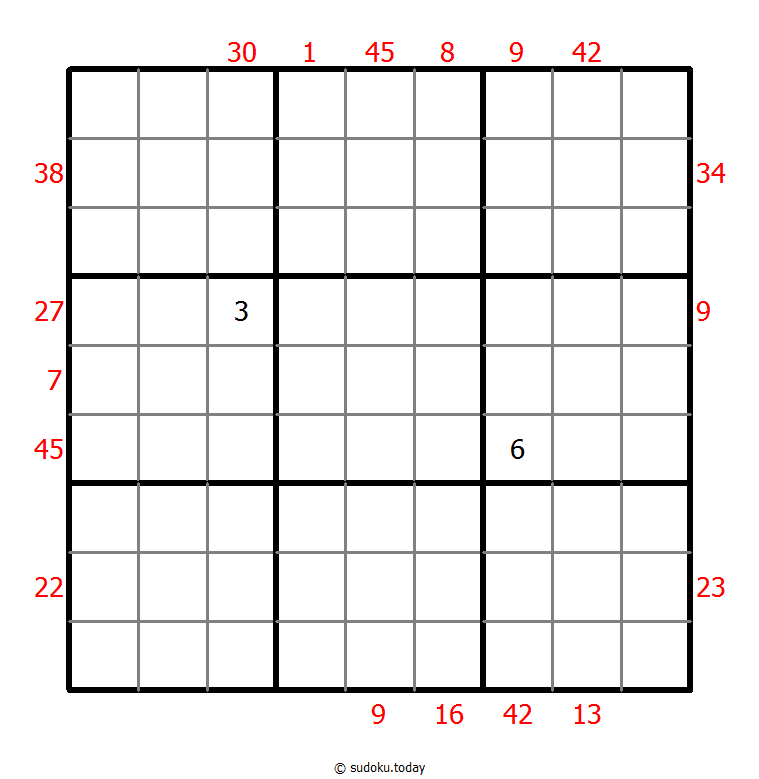
X Sums Sudoku
- Place a digit from 1 to 9 into each of the empty squares so that each digit appears exactly once in each of the rows, columns and the nine outlined 3x3 regions.
- Each number outside the grid is the sum of the first X numbers placed in the corresponding direction, where X is equal to the first number placed in that direction.
Anti Knight Sudoku
- Place a digit from 1 to 9 into each of the empty squares so that each digit appears exactly once in each of the rows, columns and the nine outlined 3x3 regions.
- The same numbers are not chess-knight move connected.
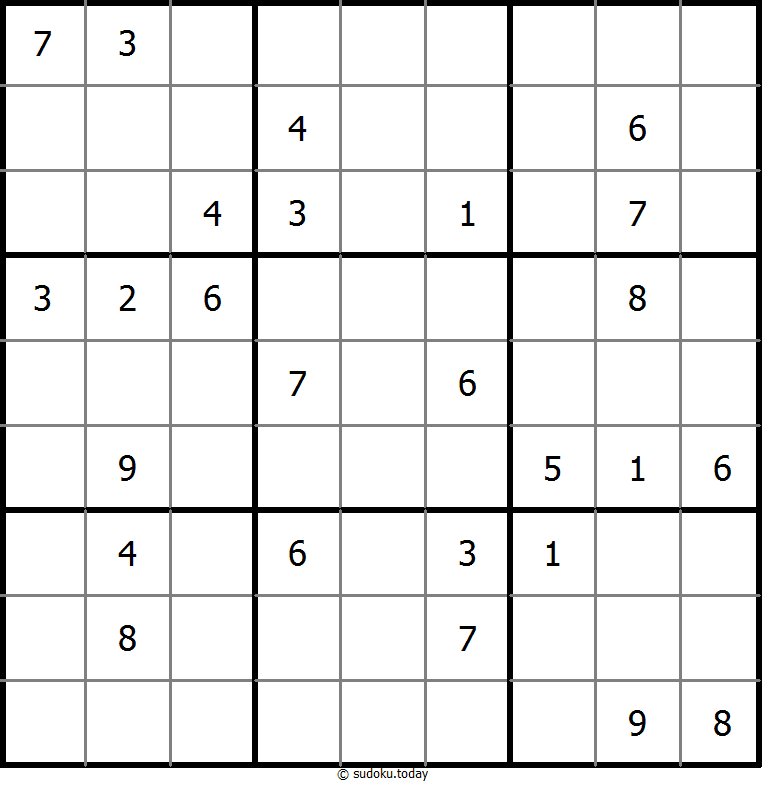
Anti Knight Sudoku
- Place a digit from 1 to 9 into each of the empty squares so that each digit appears exactly once in each of the rows, columns and the nine outlined 3x3 regions.
- The same numbers are not chess-knight move connected.
Anti Knight Sudoku
- Place a digit from 1 to 9 into each of the empty squares so that each digit appears exactly once in each of the rows, columns and the nine outlined 3x3 regions.
- The same numbers are not chess-knight move connected.
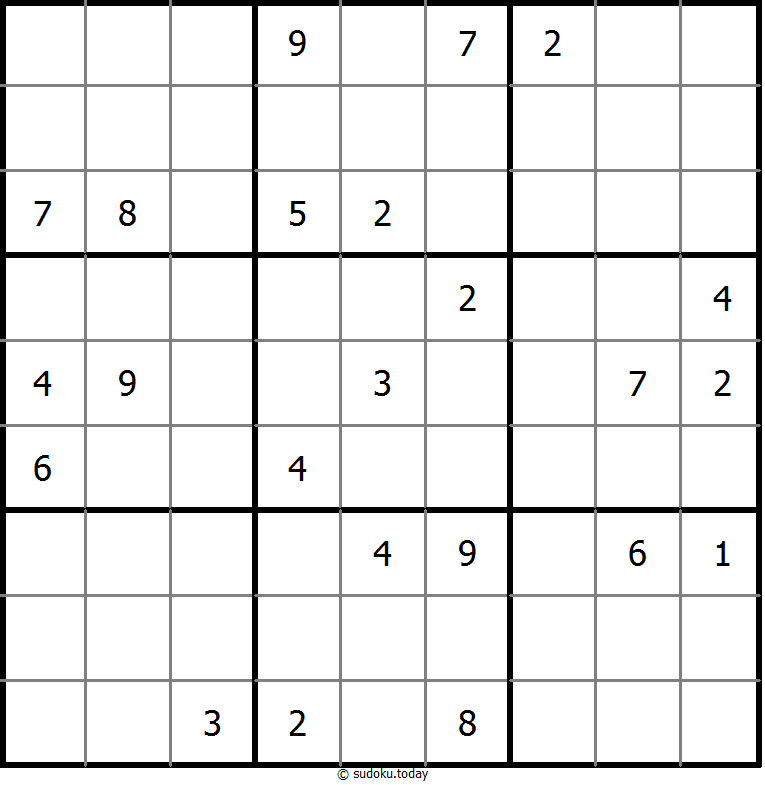
Anti Knight Sudoku
- Place a digit from 1 to 9 into each of the empty squares so that each digit appears exactly once in each of the rows, columns and the nine outlined 3x3 regions.
- The same numbers are not chess-knight move connected.
Greater Than Kropki Sudoku
- Place a digit from 1 to 9 into each of the empty squares so that each digit appears exactly once in each of the rows, columns and the nine outlined 3x3 regions.
- In all cases where two digits have a consecutive value or one digit is two times as big as the other digit (or both), a greater than sign is placed. Digits have to be placed in accordance with the sign.
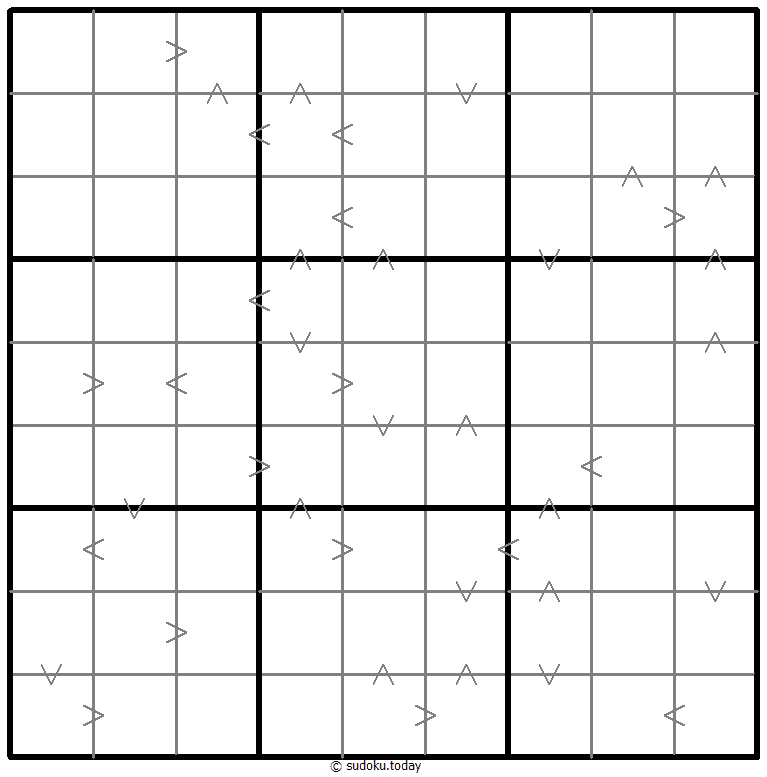
Greater Than Kropki Sudoku
- Place a digit from 1 to 9 into each of the empty squares so that each digit appears exactly once in each of the rows, columns and the nine outlined 3x3 regions.
- In all cases where two digits have a consecutive value or one digit is two times as big as the other digit (or both), a greater than sign is placed. Digits have to be placed in accordance with the sign.
Arrow Sudoku
- Place a digit from 1 to 9 into each of the empty squares so that each digit appears exactly once in each of the rows, columns and the nine outlined 3x3 regions.
- The sum of the digits along the path of each arrow equals the digit in the circled cell. Digits may repeat within an arrow shape.
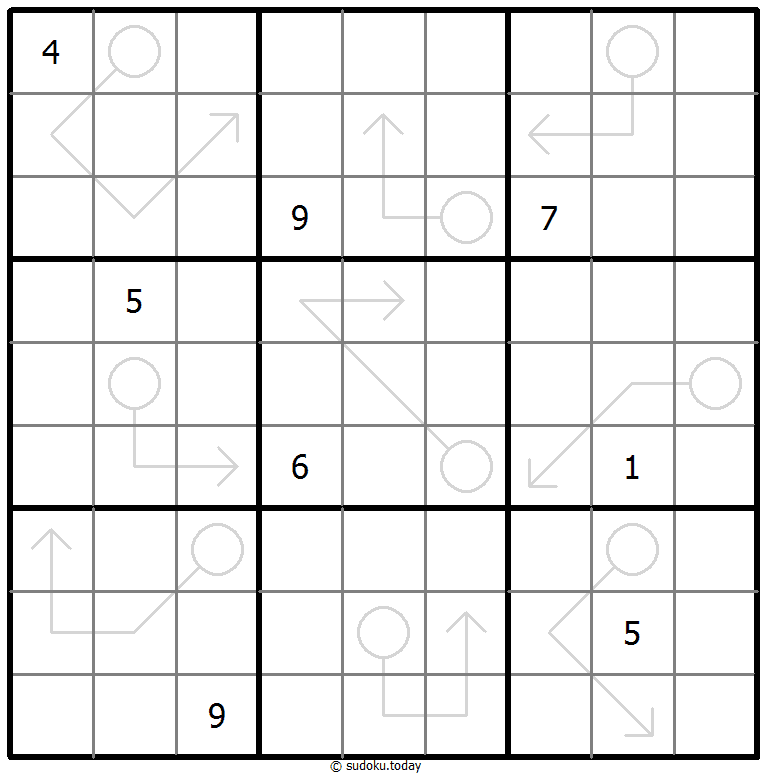
Arrow Sudoku
- Place a digit from 1 to 9 into each of the empty squares so that each digit appears exactly once in each of the rows, columns and the nine outlined 3x3 regions.
- The sum of the digits along the path of each arrow equals the digit in the circled cell. Digits may repeat within an arrow shape.
Clone Sudoku
- Place a digit from 1 to 9 into each of the empty squares so that each digit appears exactly once in each of the rows, columns and the nine outlined 3x3 regions.
- Grey cells in the grid represent many cloned areas. Digits in these areas on corresponding positions must be identical. Cloned areas are only moved, without rotation or reflection.

Clone Sudoku
- Place a digit from 1 to 9 into each of the empty squares so that each digit appears exactly once in each of the rows, columns and the nine outlined 3x3 regions.
- Grey cells in the grid represent many cloned areas. Digits in these areas on corresponding positions must be identical. Cloned areas are only moved, without rotation or reflection.
Skyscrapers Sudoku
- Place a digit from 1 to 9 into each of the empty squares so that each digit appears exactly once in each of the rows, columns and the nine outlined 3x3 regions.
- Consider each number to be the height of a building. The numbers outside the grid indicate how many buildings can be seen when looking in that direction (taller buildings conceal smaller buildings behind them).
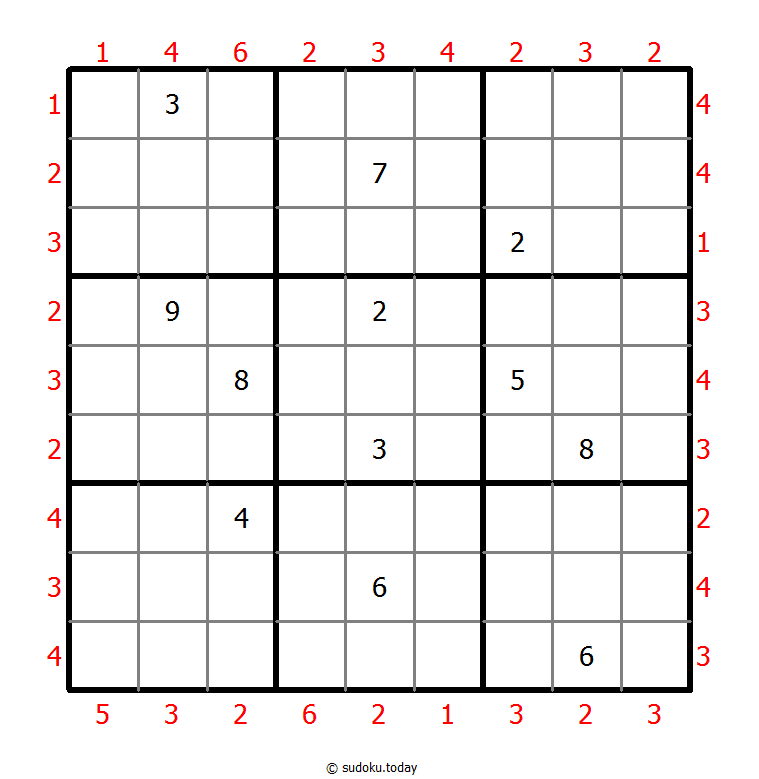
Skyscrapers Sudoku
- Place a digit from 1 to 9 into each of the empty squares so that each digit appears exactly once in each of the rows, columns and the nine outlined 3x3 regions.
- Consider each number to be the height of a building. The numbers outside the grid indicate how many buildings can be seen when looking in that direction (taller buildings conceal smaller buildings behind them).
Consecutive Sudoku
- Place a digit from 1 to 9 into each of the empty squares so that each digit appears exactly once in each of the rows, columns and the nine outlined 3x3 regions.
- There are some dots between cells. The numbers on each side of a dot must always be consecutive. All possible dots are marked.
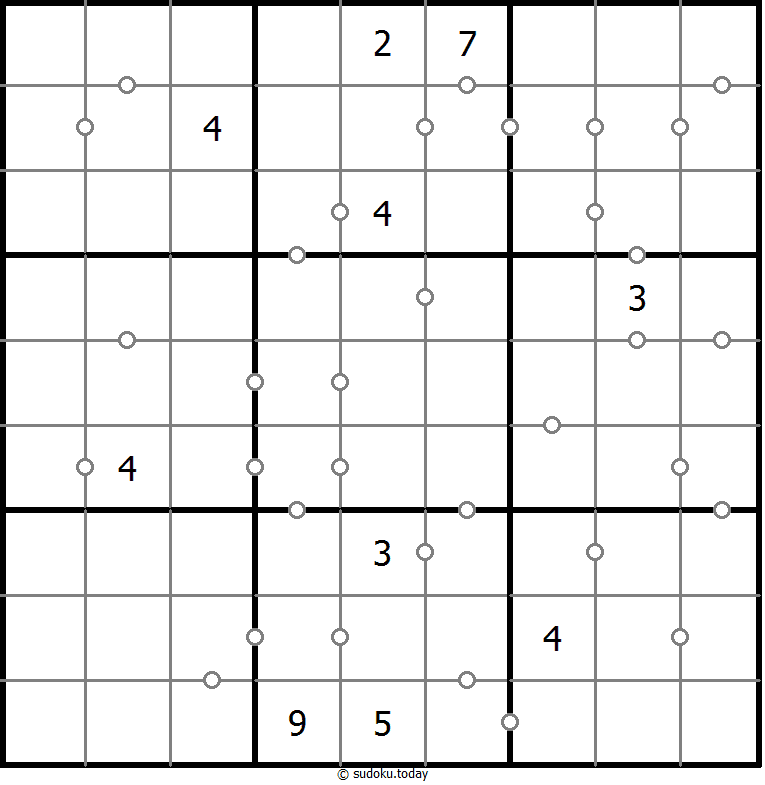
Consecutive Sudoku
- Place a digit from 1 to 9 into each of the empty squares so that each digit appears exactly once in each of the rows, columns and the nine outlined 3x3 regions.
- There are some dots between cells. The numbers on each side of a dot must always be consecutive. All possible dots are marked.
Multi Diagonal Sudoku
- Place a digit from 1 to 9 into each of the empty squares so that each digit appears exactly once in each of the rows, columns and the nine outlined 3x3 regions.
- Digits do not repeat along the marked diagonals.
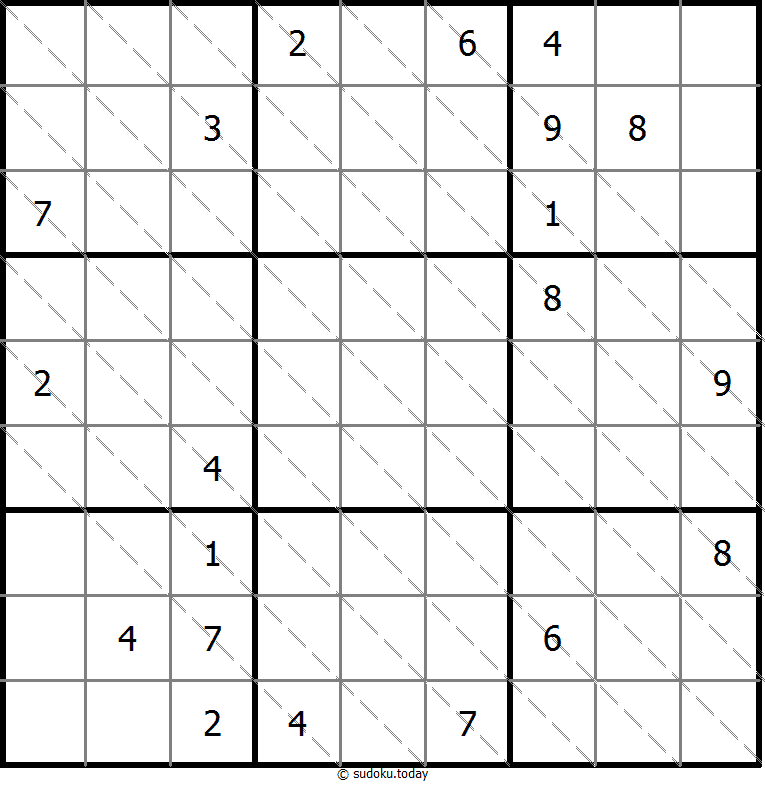
Multi Diagonal Sudoku
- Place a digit from 1 to 9 into each of the empty squares so that each digit appears exactly once in each of the rows, columns and the nine outlined 3x3 regions.
- Digits do not repeat along the marked diagonals.
Neighbourship Sudoku
- Place a digit from 1 to 9 into each of the empty squares so that each digit appears exactly once in each of the rows, columns and the nine outlined 3x3 regions.
- A number in a squared cell indicates how many different numbers the four diagonally adjacent cells contain. A number in a circled cell indicates how many different numbers the eight orthogonally and diagonally adjacent cells contain.
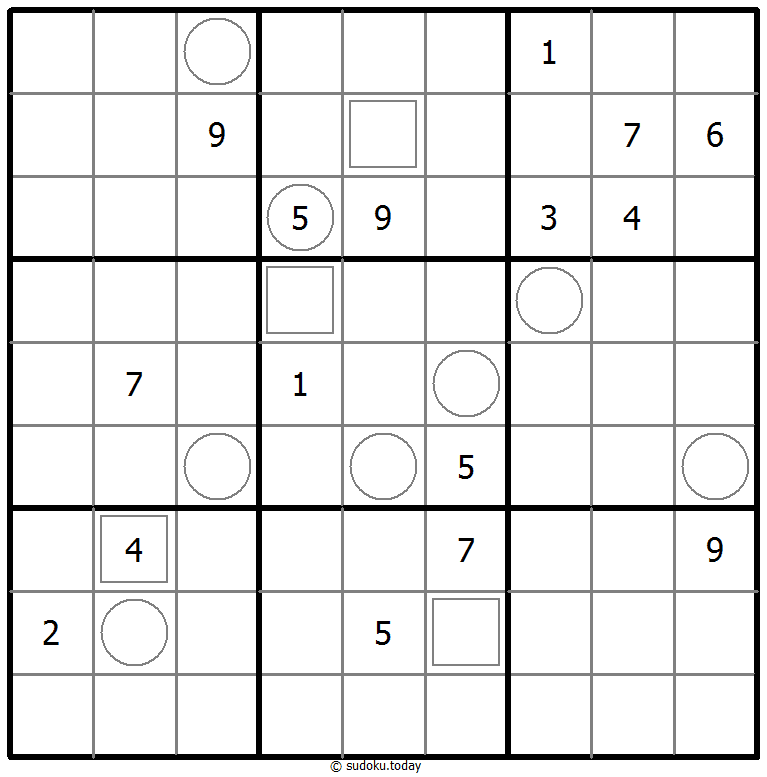
Neighbourship Sudoku
- Place a digit from 1 to 9 into each of the empty squares so that each digit appears exactly once in each of the rows, columns and the nine outlined 3x3 regions.
- A number in a squared cell indicates how many different numbers the four diagonally adjacent cells contain. A number in a circled cell indicates how many different numbers the eight orthogonally and diagonally adjacent cells contain.
Greater Than Kropki Sudoku
- Place a digit from 1 to 9 into each of the empty squares so that each digit appears exactly once in each of the rows, columns and the nine outlined 3x3 regions.
- In all cases where two digits have a consecutive value or one digit is two times as big as the other digit (or both), a greater than sign is placed. Digits have to be placed in accordance with the sign.
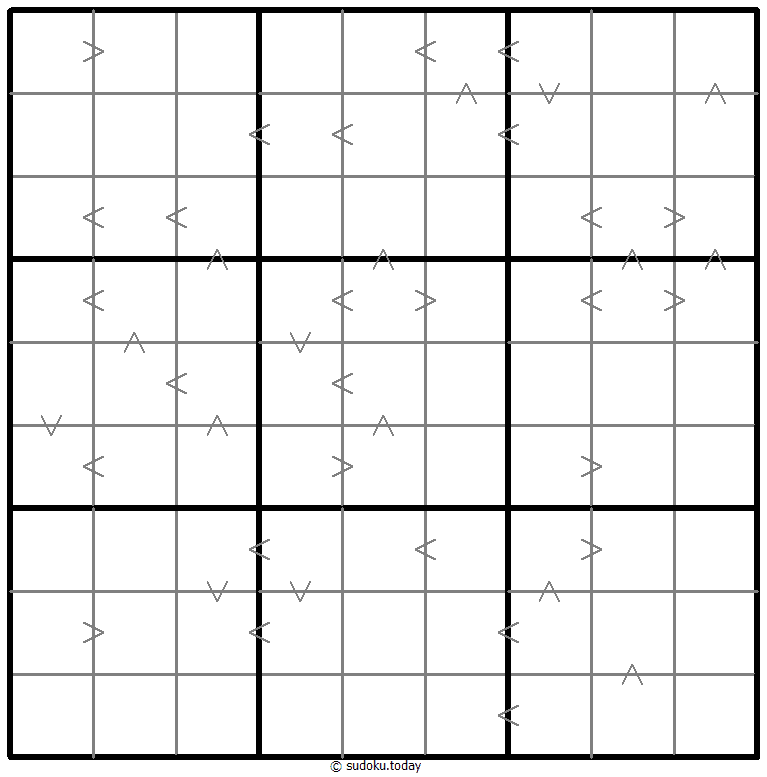
Greater Than Kropki Sudoku
- Place a digit from 1 to 9 into each of the empty squares so that each digit appears exactly once in each of the rows, columns and the nine outlined 3x3 regions.
- In all cases where two digits have a consecutive value or one digit is two times as big as the other digit (or both), a greater than sign is placed. Digits have to be placed in accordance with the sign.
Extra Regions Sudoku
- Place a digit from 1 to 9 into each of the empty squares so that each digit appears exactly once in each of the rows, columns and the nine outlined 3x3 regions.
- The connected shaded cells contain each digit from 1 to 9.

Extra Regions Sudoku
- Place a digit from 1 to 9 into each of the empty squares so that each digit appears exactly once in each of the rows, columns and the nine outlined 3x3 regions.
- The connected shaded cells contain each digit from 1 to 9.
Group Sum Sudoku
- Place a digit from 1 to 9 into each of the empty squares so that each digit appears exactly once in each of the rows, columns and the nine outlined 3x3 regions.
- Each number at the intersection of four cells is the sum of digits in those four cells.
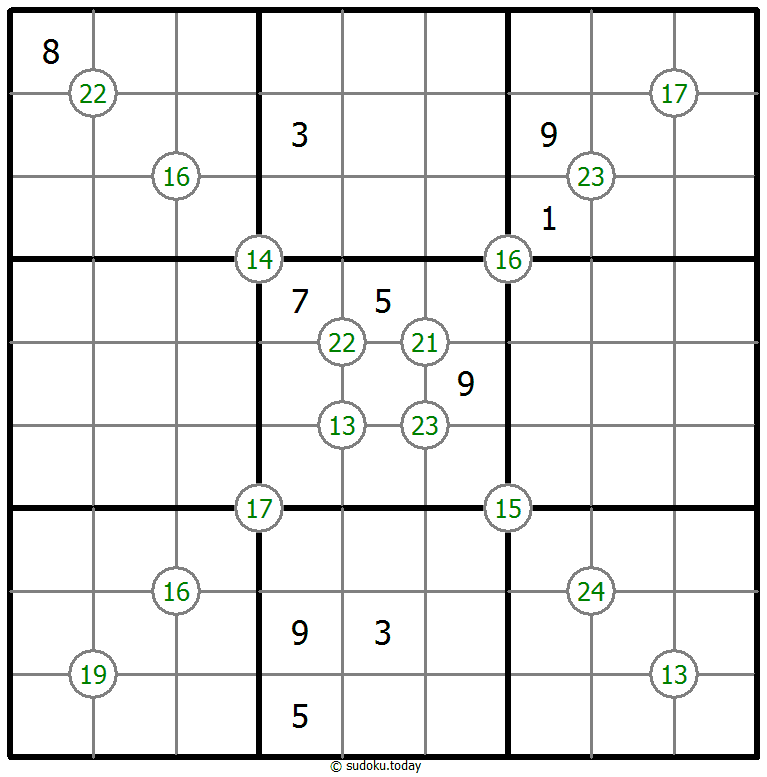
Group Sum Sudoku
- Place a digit from 1 to 9 into each of the empty squares so that each digit appears exactly once in each of the rows, columns and the nine outlined 3x3 regions.
- Each number at the intersection of four cells is the sum of digits in those four cells.
Sum Frame Sudoku
- Place a digit from 1 to 9 into each of the empty squares so that each digit appears exactly once in each of the rows, columns and the nine outlined 3x3 regions.
- Digits outside the grid indicate the sum of the first 3 digits in the corresponding direction.
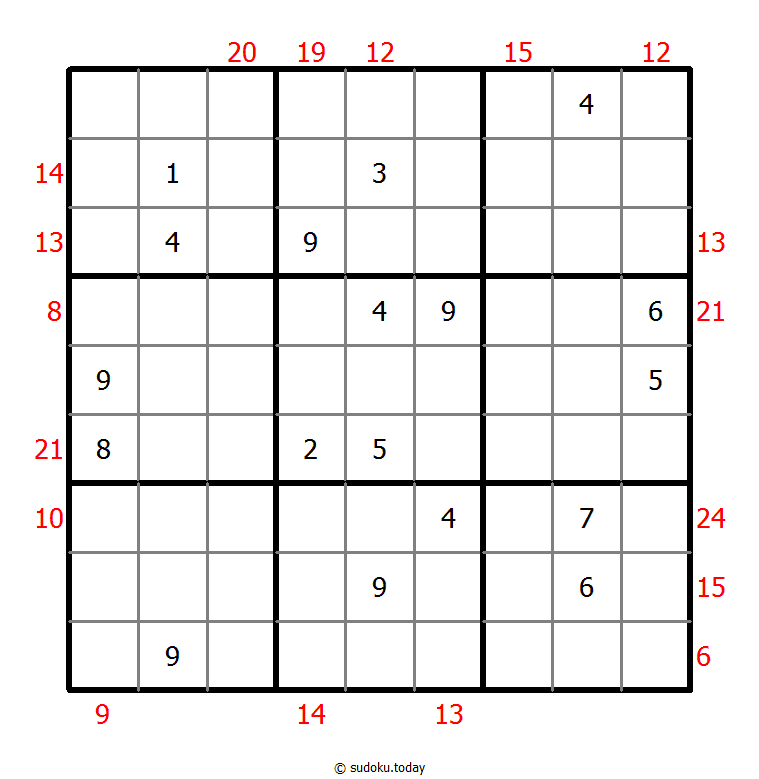
Sum Frame Sudoku
- Place a digit from 1 to 9 into each of the empty squares so that each digit appears exactly once in each of the rows, columns and the nine outlined 3x3 regions.
- Digits outside the grid indicate the sum of the first 3 digits in the corresponding direction.
Windoku
- Place a digit from 1 to 9 into each of the empty squares so that each digit appears exactly once in each of the rows, columns and the nine outlined 3x3 regions.
- Each of the four shaded 3x3 boxes contains each digit from 1 to 9.

Windoku
- Place a digit from 1 to 9 into each of the empty squares so that each digit appears exactly once in each of the rows, columns and the nine outlined 3x3 regions.
- Each of the four shaded 3x3 boxes contains each digit from 1 to 9.
Parity Lines Sudoku
- Place a digit from 1 to 9 into each of the empty squares so that each digit appears exactly once in each of the rows, columns and the nine outlined 3x3 regions.
- Digits along each marked line are either all odd or all even.
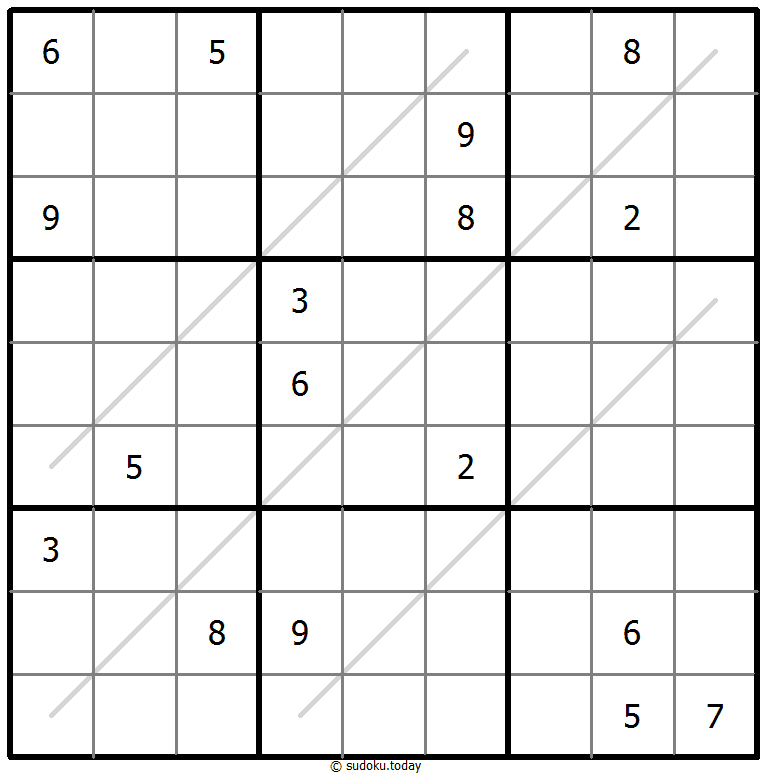
Parity Lines Sudoku
- Place a digit from 1 to 9 into each of the empty squares so that each digit appears exactly once in each of the rows, columns and the nine outlined 3x3 regions.
- Digits along each marked line are either all odd or all even.